 |
y-cruncher Multi-Precision Library |
 |
A Multi-threaded Multi-Precision Arithmetic Library(Powered by y-cruncher) |
(Last updated: March 14, 2016)
YMP Large Multiplication Benchmarks
When it comes to bignum libraries, nearly everything reduces to large integer multiplication. So not surprisingly, multiplication is really the only thing that matters in terms of performance...
Just as with individual processor instructions, there are two benchmarks what we care about: latency and throughput
- Latency is how long it takes to perform a single multiplication of size N while running alone on the processor.
- Throughput is how many multiplications of size N that can be sustained in unit time using the entire processor.
Historically, latency is all the only thing that mattered. But in the multi-core era, throughput becomes more important for threaded applications.
Intuitively, one would think that thoughput can be calculated from the latency based on the number of cores. But this simple model fails to take into account for shared resources such as cache and memory bandwidth. Quite often, what's optimal for latency can be inefficient for throughput. For example, FFTs may be the fastest thing for latency. But they scale terribly in a multi-threaded environment due to saturation of memory bandwidth.
YMP is optimized for throughput rather than latency.
Benchmark Disclaimer:
Since everyone loves to use GMP as a baseline for bignum performance, we will do the same. But be aware that these benchmarks are not exactly apples-to-apples comparisons. GMP is a sequential program that supports no parallelism. YMP is both threaded and vectorized.
While this doesn't make for a very fair comparison, the reality is that modern systems are becoming increasingly parallel in a manner that is "use it or lose it".
Integer Multiplication Latency:
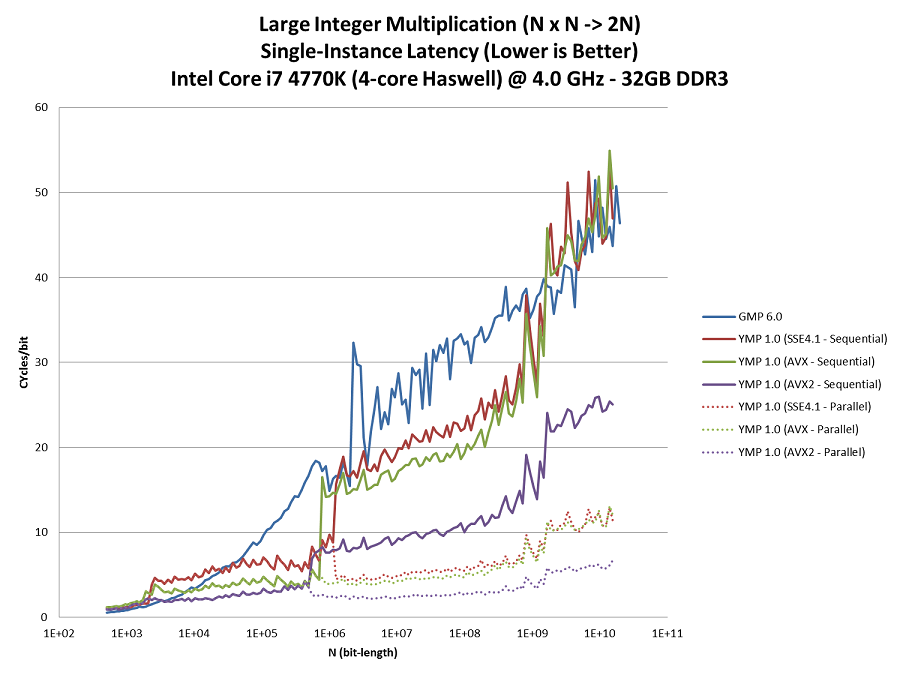
The graph above plots the latency of a single N x N-bit integer multiplication. The y-axis is the run-time in processor cycles scaled by the input size.
For example, the largest data point for GMP is 223 seconds for N = 17,613,024,960.
Since the processor runs at 4 GHz, the "cycles/bit" is computed as: (223 * 4,000,000,000) / 17,613,024,960 = 50.6 cycles/bit
The GMP benchmarks were done in Ubuntu Linux using this program: bench_gmp_multiply_latency.cpp
The YMP benchmarks were done in Windows 7 using the Number Factory app: https://github.com/Mysticial/NumberFactory
Observations:
- Vectorization matters a lot.
- Parallelization matters even more. But YMP doesn't attempt to parallelize until the size crosses a threshold.
- YMP is only faster than GMP for sizes above 104 bits or so. It's difficult to beat GMP's hand-tuned assembly for these smaller sizes.
- With AVX2, YMP is about 2 - 3x faster than GMP per thread.
- With AVX2 and multi-threading, YMP can be over 10x faster than GMP. (Note that this is a quad-core processor with Hyperthreading.)
Integer Multiplication Throughput:
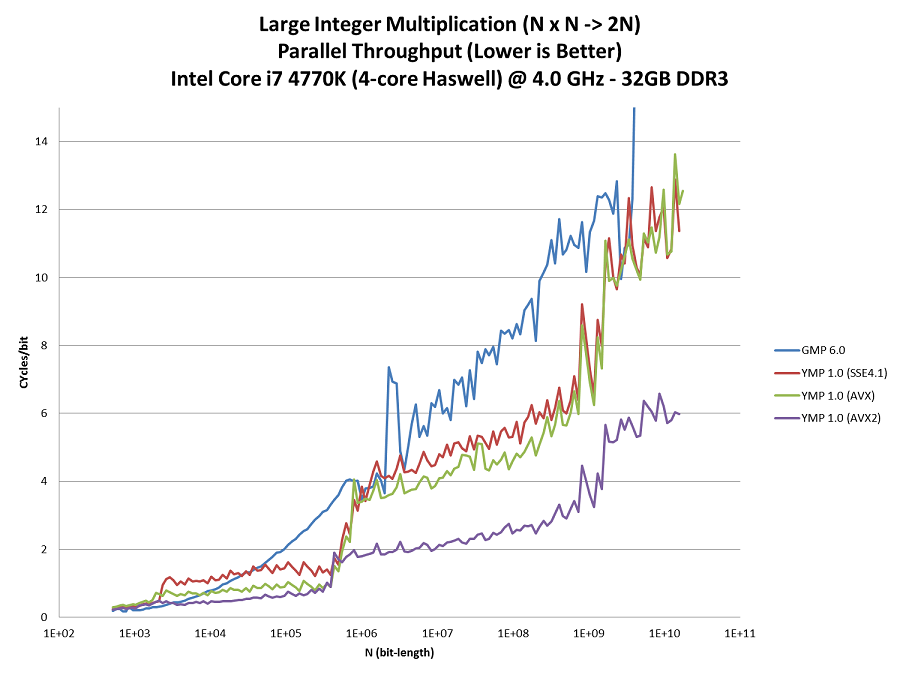
This graph plots the throughput of N x N-bit integer multiplications. Again the y-axis is the run-time in processor cycles scaled by the input size.
The goal of a throughput benchmark is the perform as many multiplications as possible in unit time. The best way to do this on an N core processor is to have N threads loop independent iterations since this minimizes synchronization overhead. When there is insuffient memory to run N simultaneous instances, reduce the number of instances and (if possible) use multiple threads within each instance. In other words: parallelize within the multiplication. This is something that YMP can do, but GMP currently cannot.
Throughput benchmarks are much more relevant for parallel workloads such Number Factory and y-cruncher. Small multiplications use little memory so many of them can be done in parallel. But large multiplications are large and no more than one or a few can be done concurrently with a given memory budget.
The GMP benchmarks were done in Ubuntu Linux using this program: bench_gmp_multiply_throughput.cpp
The YMP benchmarks were done in Windows 7 using the Number Factory app: https://github.com/Mysticial/NumberFactory
Observations:
GMP's performance plunges drastically above 3*109 bits. (It goes to 50 cycles/bit. That's 3x the height of the current scaling.)
Above this point, there is insufficient memory to run 4 instances. Therefore, it must run fewer. But since GMP cannot parallelize within the large multiplication, it leads to an under-utilization of the processor cores. Thus, the throughput falls off a cliff.