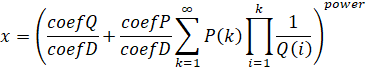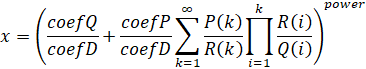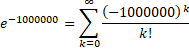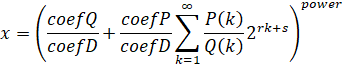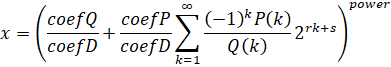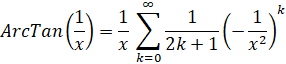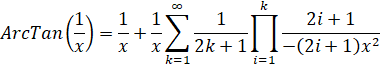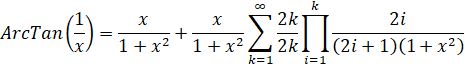User Guides - Functions List

By Alexander Yee

 

(Last updated: September 29, 2024)

 

 

Back To:

This is the function reference for the Custom Formula feature in y-cruncher.

Support Basic Arithmetic Functions Built-in Constants Binary Splitting Series Function Templates
Integer LinearCombination Invsqrt(x) GoldenRatio SeriesHyperdescent ArcTan(1/x) for integer x - Taylor Series
Scope Square Sqrt(x) E SeriesHypergeometric ArcTan(1/x) for integer x - Euler Series
  Multiply InvNthRoot Pi SeriesBinaryBBP  
  Reciprocal AGM(1,x), AGM(a,b) Log2    
  Divide Log(x) Zeta3    
  Shift Exp(x) Catalan    
  Power Hyperbolic Trig Functions Lemniscate    
    Inverse Hyperbolic Trig Functions EulerGamma    

The custom formula feature should be considered a portal to y-cruncher's internal capabilities instead of a full-out math library. So it lacks a lot of common functionality while also having some unusual and specialized functions (like the series functions).

 

Fundumentally, y-cruncher only supports:

Everything else is built on top of these. Anything that cannot be expressed as the above for real inputs is not supported.

 

*Technically not true. They can be done using the bit-burst algorithm. But this algorithm is very difficult to implement in the context of y-cruncher's infrastructure. They can also be done using Landon transforms of the Elliptic integral with the AGM, but I haven't figured out how to do this yet.

 

 

Support:

 

General support.

 

Integer:

{
    Integer : 123
}

Purpose:

Convert an integer into a large number.

 

This function is generally not needed as you can simply inline the integer instead of using the full function form. Some functions will recognize the inlined integer and switch to a faster method instead.

 

It is generally recommended to avoid auto-promoting large integers this way. New versions of y-cruncher may add optimizations for integer input that are restricted to less than the full 64-bit integer range. This will break backwards compatibility.

where:

 

Performance Metrics:

 

Scope: Scoped Variables

{
    Scope : {
        Locals : [
            {var0 : {...}}
            {var1 : {...}}
        ]
        Formula : {...}
    }
}

{
    Scope : {
        Locals : [
            {var0 : {...}}
            {var1 : {...}}
        ]
        Formula : {
            Sqrt : "var1"
        }
    }
}

Purpose:

Defines one or more local variables that can be referenced inside a scope. The sole purpose of this is to allow subexpressions to be reused.

 

The sample formula, "Universal Parabolic Constant.cfg" uses this to avoid computing Sqrt(2) twice.

 

Variables are defined inside the "Locals" node. Once defined, the variable can be referenced anywhere inside the "Formula" node including all sub-scopes.

Variable names must be alpha-numeric. Underscores are also allowed.

Variables of the same name in the same scope are disallowed. (The config parser will reject it anyway.)

Variables of the same name in nested scopes will shadow. The inner scope will shadow the outer scope.

 

Expressions inside the "Locals" node can reference variables defined before it in the same scope.

Tips:

 

Performance Metrics:

 

The current implementation has a limitation that forces it to copy the variable each time it is loaded - thus incurring an O(n) run-time cost. This applies to both Ram Only and Swap Mode. So loading a variable in Swap Mode will incur a disk copy. This is slated for improvement in the future.

 

The reason for this limitation has to do with return value optimization and mutability of function return values. The current internal API is that all functions return a mutable large number into a buffer provided by the caller. This allows the caller to overwrite the number if needed to reduce memory/storage consumption. However, this design is incompatible with variables since they are immutable. The current work-around is to simply copy the immutable variable into the mutable buffer.

 

 

Arithmetic:

 

Basic arithmetic.

 

LinearCombination:

{
    LinearCombination : [
        [121 {...}]
        [-10 {...}]
        [654 {...}]
    ]
}

This is a variable-input function that will accept any number of operands.

 

 

Computes:

a0*x0 + a1*x1 + a2*x2 + ...

where:

 

Tips:

 

Performance Metrics:

Metric Addition Multiply by Coefficient Multiply by 1 or -1
Computational Cost O(n) O(1)
Auxiliary Memory O(n) O(1) O(1)

 

Square: Multiply Number by Itself. (New in: y-cruncher v0.8.4)

{
    Square : {...}
}

Computes:

x2

where:

 

Tips:

 

Performance Metrics:

Metric Large Multiply
Computational Cost M(n)
O(n log(n))
Auxiliary Memory O(n)

 

Multiply: Large Multiplication

{
    Multiply : [
        {...}
        {...}
        {...}
    ]
}

This is a variable-input function that will accept any number of operands.

 

 

Computes:

x0 * x1 * x2 * x3 ...

where:

 

Tips:

 

Performance Metrics:

Metric Large Multiply
Computational Cost M(n)
O(n log(n))
Auxiliary Memory O(n)

 

Reciprocal: 1 / x (New in: y-cruncher v0.8.4)

{
    Reciprocal : {...}
}

Computes:

1 / x

where:

 

Tips:

 

Performance Metrics:

Metric Divide by Integer Divide by Large Number
Computational Cost   1.667 M(n)
O(n) O(n log(n))
Auxiliary Memory O(n) O(n)

 

Divide: Division

{
    Divide : [
        {...}
        123
    ]
}

{
    Divide : [
        {...}
        {...}
    ]
}

Computes:

x0 / x1

 

Tips:

 

Performance Metrics:

Metric Divide by Integer Divide by Large Number
Computational Cost   2.167 M(n)
O(n) O(n log(n))
Auxiliary Memory O(n) O(n)

 

Shift: Multiply/Divide by Power-of-Two

{
    Shift : [
        {...}
        -12
    ]
}

Multiply the 1st operand by a power-of-two indicated by the 2nd operand.

 

 

Computes:

arg[0] * 2arg[1]

where:

Tips:

 

Performance Metrics:

Metric Power not divisible by word size Power divisible by word size
Computational Cost O(n) O(1)
Auxiliary Memory O(1) O(1)

 

Power: Power Function

{
    Power : [
        {...}
        -3
    ]
}

{
    Power : [
        {...}
        {...}
    ]
}

{
    Power : {
        Base: {...}
        Exponent: {...}
        Pi: {...}
        Log2: {...}
    }
}

Computes:

arg[0]arg[1]

 

baseexponent

 

The 1st version is a simple integer power function.

The 2nd version is the fully generic non-integer power function.

 

For non-integer exponents, this function internally requires the constants Pi and Log2. If these constants are also needed elsewhere, you can define them in an enclosing Scope and pass them in as parameters using the 3rd version of this function.

 

Both the "Pi" and "Log2" parameters are optional. If you omit one, it will automatically be computed internally. If you do provide them, they must be the correct values.

 

Restrictions:

 

Tips:

 

Performance Metrics:

Metric

Power = 2

(Square)

Power = -1

(Reciprocal)

 Positive Power Negative Power Non-Integer Power
Computational Cost 0.667 M(n) 1.667 M(n) varies very slow
O(n log(n)) O(N log(N) log(|power|)) O(n log(n)3)
Auxiliary Memory O(N) O(N) O(N)

For integer powers, the current implementation of this function is straight-forward binary exponentiation. If the binary representation of the exponent has a lot of 1 bits, it may be faster to use alternate representations of the power - such as factoring the exponent and doing nested calls.

 

For non-integer powers, it calls:

Exp( exponent * Log(base) )

 

 

Functions:

 

Elementary and transcendental functions.

 

Invsqrt: Inverse Square Root

{
    Invsqrt : 23
}

{
    Invsqrt : {...}
}

Computes:

1 / sqrt(x)

where:

 

Performance Metrics:

Metric Integer Input Large Input
Computational Cost 1.333 M(n) 2.833 M(n)
O(n log(n))
Auxiliary Memory O(n)

y-cruncher's implementation for large inverse square roots is not well optimized.

 

Sqrt: Square Root

{
    Sqrt : 23
}

{
    Sqrt : {...}
}

Computes:

sqrt(x)

where:

Tips:

 

Performance Metrics:

Metric Integer Input Large Input
Computational Cost 1.333 M(n) 3.833 M(n)
O(n log(n))
Auxiliary Memory O(n)

y-cruncher's implementation for large square roots is not well optimized.

 

 

InvNthRoot: Inverse Nth Root

{
    InvNthRoot : [23 {...}]
}

Computes:

Computes the reciprocal radical of Nth degree.

 

arg[1]-1/arg[0]

 

Taking the Nth root of any negative number will result in an error - even if the degree is odd. Even though y-cruncher doesn't support complex numbers, it will adhere to standard branch cut conventions. Thus raising any negative number to a non-integral power will put it off the real number line thereby resulting in a complex number. And since y-cruncher doesn't support complex numbers, it will simply error.

where:

Tips:

 

Performance Metrics:

Metric Inverse Nth Root
Computational Cost O(N log(N) log(degree))
Auxiliary Memory O(n)

 

 

AGM: Arithmetic-Geometric Mean

{
    AGM : {...}
}

{
    AGM : [
        {...}
        {...}
    ]
}

Computes:

Computes the Arithmetic-Geometric Mean.

where:

 

Performance Metrics:

 

Be aware that the AGM has a very large Big-O constant and is extremely memory intensive. So it is very slow on bandwidth-constrained systems and has terrible performance in swap mode. For constants that can be computed with both the AGM and a hypergeometric series, it is often the case that the AGM implementation will be faster in memory, but slower than the hypergeometric series in swap mode.

Metric Complexity
Computational Cost 4.833 lg(n) M(n)*
O(n log(n)2)
Auxiliary Memory O(n)

*This assumes that the two inputs are roughly the same in magnitude. The cost will go up if there is a large difference in magnitude.

 

y-cruncher's implementation for the AGM is not well optimized. Part of it is inherited from the unoptimized square root inplementation.

 

Log: Natural Logarithm

{
    Log : 10
}

{
    Log : {...}
}

(New in: y-cruncher v0.8.4)
{
    Log : {
        x: {...}
        Pi : {...}
        Log2 : {...}
    }
}

Computes:

Natural logarithm of x.

 

 

(New in: y-cruncher v0.8.4)

 

For non-integer x, this function internally requires the constants Pi and Log2. If these constants are also needed elsewhere, you can define them in an enclosing Scope and pass them in as parameters using the 3rd version of this function.

 

Both the "Pi" and "Log2" parameters are optional. If you omit one, it will automatically be computed internally. If you do provide them, they must be the correct values.

where:

 

Performance Metrics:

Metric Complexity
Computational Cost 9.666 lg(n) M(n) + cost(Pi) + cost(log(2))
O(n log(n)3)
Auxiliary Memory O(n)

 

Exp: Exponential Function (New in: y-cruncher v0.8.4)

{
    Exp : 10
}

{
    Exp : {...}
}

{
    Exp : {
        x: 10
        e : {...}
    }
}

{
    Exp : {
        x: {...}
        Pi : {...}
        Log2 : {...}
    }
}

Computes:

ex

 

For integer x, this function internally requires the constant e as an input. If this constant is also needed elsewhere, you can define it in an enclosing Scope and pass it in as a parameter using the 3rd version of this function.

 

For non-integer x, this function internally requires the constants Pi and Log2. If these constants are also needed elsewhere, you can define them in an enclosing Scope and pass them in as parameters using the 4th version of this function.

 

Both the "Pi" and "Log2" parameters are optional. If you omit one, it will automatically be computed internally. If you do provide them, they must be the correct values.

 

Performance Metrics:

Metric Complexity
Computational Cost 19.333 lg(n) M(n) + cost(Pi) + cost(log(2))
O(n log(n)3)
Auxiliary Memory O(n)

 

Hyperbolic Trigonometric Functions (New in: y-cruncher v0.8.4)

{
    Tanh : {...}
}
{
    Tanh : {
        x : {...}
        Pi : {...}
        Log2 : {...}
    }
}

Computes:

Sinh(x) - Hyperbolic Sine

Cosh(x) - Hyperbolic Cosine

Tanh(x) - Hyperbolic Tangent

Coth(x) - Hyperbolic Cotangent

Sech(x) - Hyperbolic Secant

Csch(x) - Hyperbolic Cosecant

 

Each of these functions can be called with a single parameter which is x.

 

For non-integer x, these functions internally require the constants Pi and Log2. If these constants are also needed elsewhere, you can define them in an enclosing Scope and pass them in as parameters using the 2nd version of this function.

 

Both the "Pi" and "Log2" parameters are optional. If you omit one, it will automatically be computed internally. If you do provide them, they must be the correct values.

 

Performance Metrics:

Metric Complexity
Computational Cost O(n log(n)3)
Auxiliary Memory O(n)

Everything else is implemented as their definitions in terms of Exp(x).

 

 

Inverse Hyperbolic Trigonometric Functions (New in: y-cruncher v0.8.4)

{
    ArcTanh : {...}
}
{
    ArcTanh : {
        x : {...}
        Pi : {...}
        Log2 : {...}
    }
}



(ArcCoth Only)
{
    ArcCoth : {
        Coefficient : 18
        x : 26
    }
}

Computes:

ArcSinh(x) - Inverse Hyperbolic Sine

ArcCosh(x) - Inverse Hyperbolic Cosine

ArcTanh(x) - Inverse Hyperbolic Tangent

ArcCoth(x) - Inverse Hyperbolic Cotangent

ArcSech(x) - Inverse Hyperbolic Secant

ArcCsch(x) - Inverse Hyperbolic Cosecant

 

Each of these functions can be called with a single parameter which is x.

 

ArcCoth(x) has a special version for integers that computes Coefficient * ArcCoth(x). This exposes the native function that's used for Machin-like Log(x) formulas.

 

These functions internally require the constants Pi and Log2. If these constants are also needed elsewhere, you can define them in an enclosing Scope and pass them in as parameters using the 2nd version of this function.

 

Both the "Pi" and "Log2" parameters are optional. If you omit one, it will automatically be computed internally. If you do provide them, they must be the correct values.

 

Performance Metrics:

Metric Complexity
Computational Cost O(n log(n)3)
Auxiliary Memory O(n)

Aside from the special case for ArcCoth(x) for integers, everything else is implemented as their definitions in terms of Log(x).

 

 

 

Built-in Constants:

 

These are y-cruncher's built-in implementations for all the constants. Some of these also expose the secondary algorithms. This is to help construct computationally independent formulas for the usual compute+verify process.

 

GoldenRatio: φ

{
    GoldenRatio : {}
}

{
    GoldenRatio : {
        Power : -1
    }
}

Computes:

φpower

 

φ = 1.61803398874989484820458683436563811772030917980576...

where:

 

Performance Metrics:

Metric Complexity
Computational Cost 1.333 M(n)
O(n log(n))
Auxiliary Memory O(n)

 

E

{
    E : {}
}

{
    E : {
        Power : -1
    }
}

Computes:

epower

 

e = 2.71828182845904523536028747135266249775724709369995...

where:

There's no option here to select the algorithm. Internally, it uses:

In other words, it uses the alternating series when power is -1.

 

 

Performance Metrics:

Metric Complexity
Computational Cost O(n log(n)2)
Auxiliary Memory O(n)

 

Pi

{
    Pi : {}
}

{
    Pi : {
        Power : -1
        Algorithm : "chudnovsky"
    }
}

Computes:

Pipower

 

Pi = 3.14159265358979323846264338327950288419716939937510...

where:

 

Performance Metrics:

Metric Both Algorithms
Computational Cost O(n log(n)3)
Auxiliary Memory O(n)

 

Log2: Natural log of 2 (New in: y-cruncher v0.8.4)

{
    Log2 : {}
}

{
    Log2 : {
        Algorithm : "zuniga2024ii"
    }
}

Computes:

Log(2) = 0.69314718055994530941723212145817656807550013436025...

where:

 

Performance Metrics:

Metric Both Algorithms
Computational Cost O(n log(n)3)
Auxiliary Memory O(n)

 

 

Zeta3: Apery's Constant ζ(3)

{
    Zeta3 : {}
}

{
    Zeta3 : {
        Power : -1
        Algorithm : "zuniga2023vi"
    }
}

Computes:

ζ(3)power

 

ζ(3) = 1.20205690315959428539973816151144999076498629234049...

where:

 

Performance Metrics:

Metric Both Algorithms
Computational Cost O(n log(n)3)
Auxiliary Memory O(n)

 

Catalan: Catalan's Constant

{
    Catalan : {}
}

{
    Catalan : {
        Power : -1
        Algorithm : "pilehrood-short"
    }
}

Computes:

Catalanpower

 

Catalan = 0.91596559417721901505460351493238411077414937428167...

where:

There are no plans to expose the remaining built-in algorithms since they will probably be removed in the future anyway.

 

 

Performance Metrics:

Metric Both Algorithms
Computational Cost O(n log(n)3)
Auxiliary Memory O(n)

 

Lemniscate: Arc length of the Unit Lemniscate

{
    Lemniscate : {}
}

{
    Lemniscate : {
        Power : -1
        Algorithm : "zuniga2023x"
    }
}

Computes:

Lemniscatepower

 

Lemniscate Constant = 5.24411510858423962092967917978223882736550990286324...

where:

 

Performance Metrics:

Metric All Algorithms
Computational Cost O(n log(n)3)
Auxiliary Memory O(n)

 

EulerGamma: Euler-Mascheroni Constant

{
    EulerGamma : {}
}


(New in: y-cruncher v0.8.4)

{
    EulerGamma : {
        Algorithm : "brent-refined"
        Log2 : {...}
    }
}

Computes:

Euler-Mascheroni Constant = 0.57721566490153286060651209008240243104215933593992...

 

This function internally requires the constant Log2. If this constant is also needed elsewhere, you can define it in an enclosing Scope and pass it in as a parameter using the 2nd version of this function.

 

The "Log2" parameter is optional. If you omit it, it will automatically be computed internally. If you do provide it, it must be the correct value.

where:

For a fixed # of digits, the two algorithms will always pick a different n parameter. This ensures that they are computationally independent and can be used for compute+verify computation pairs.

 

 

Performance Metrics:

Metric Both Algorithms
Computational Cost O(n log(n)3)
Auxiliary Memory O(n)

 

This function is the only way to access the Euler-Mascheroni Constant. As of 2018, there are no known formulas for this constant that can be expressed as a finite combination of the other functionality in the custom formulas feature.

 

 

 

Binary Splitting Series:

 

This section covers the various Binary Splitting routines that y-cruncher supports.

 

SeriesHyperdescent

{
    SeriesHyperdescent : {
        Power : -1
        CoefficientP : 1
        CoefficientQ : 1
        CoefficientD : 1
        PolynomialP : [1]
        PolynomialQ : [0 -2 -4]
    }
}

This provides access to y-cruncher's Hyperdescent Binary Splitting framework. This is an optimized special case of SeriesHypergeometric where R(x) is 1 or -1.

This series type is really only useful for computing e, but it can also be used to efficiently compute silly stuff like:

 

Computes:

Given:

The polynomials are arrays of the coefficients in increasing order of degree. The 1st element is the constant.

 

Basic Restrictions:

Polynomial Restrictions:

  1. P(x) and Q(x) are non-zero polynomials.
  2. Q(x) must be degree 1 or higher.
  3. Q(x) is of degree no higher than 62.
  4. The coefficients of both polynomials are signed 64-bit integers: [-263, 263)
  5. The coefficient of the highest degree is non-zero for both polynomials. (no leading zeros)
  6. Q(x) is non-zero for all positive integers.

 

Tips:

 

Performance Metrics:

Metric Complexity
Computational Cost O(n log(n)2)
Auxiliary Memory O(n)

Notes:

 

SeriesHypergeometric

{
    SeriesHypergeometric : {
        Power : -1
        CoefficientP : 1
        CoefficientQ : 2
        CoefficientD : 2
        PolynomialP : [0 0 0 2 3]
        PolynomialQ : [-1 -6 -12 -8]
        PolynomialR : [0 0 0 1]
    }
}

This provides access to y-cruncher's CommonP2B3 Binary Splitting framework. This is a generic series type that allows summation of any hypergeometric series of rationals - subject to restrictions such as convergence and implementation limits.

 

 

Computes:

Given:

The polynomials are arrays of the coefficients in increasing order of degree. The 1st element is the constant.

Admittedly, this formula may be inconvenient since it does not match the conventional definition of the hypergeometric function. But it was chosen because it matches the implementation. So it is close to metal and any optimizations that are done to the formula will mirror the actual performance improvements. This representation is also slightly more general in that you can use irreducible polynomials that will not factor into a normal rational hypergeometric function.

 

 

Basic Restrictions:

Polynomial Restrictions:

  1. P(x), Q(x), and R(x) are non-zero polynomials.
  2. Q(x) must be degree 1 or higher.
  3. Q(x) and R(x) are of degree no higher than 62.
  4. The coefficients of all polynomials are signed 64-bit integers: [-263, 263)
  5. The coefficient of the highest degree is non-zero for all 3 polynomials. (no leading zeros)
  6. Q(x) and R(x) are non-zero for all positive integers.
  7. |R(x) / Q(x)| < 0.75 for all x >= 1.

The last restriction enforces a minimum rate of convergence on the series. This restriction is rather broad as it will exclude a large number of valid and convergent series. But unfortunately, it is needed for y-cruncher to work correctly.

 

For example, y-cruncher will reject the following convergent series:

This series diverges for the first 1,000,000 terms before it starts to converge. Furthermore, it exhibits destructive cancellation. This is quite typical of Confluent Hypergeometric series for large inputs. But as of version 0.7.7, y-cruncher cannot handle them and will reject all of such series.

 

 

Tips:

 

 

Performance Metrics:

Metric R(x) and Q(x) are same degree R(x) is lower degree than Q(x) R(x) is higher degree than Q(x)
Computational Cost O(n log(n)3) O(n log(n)2)

Series is Divergent
Auxiliary Memory O(n) O(n)

 

SeriesBinaryBBP

{
    SeriesBinaryBBP : {
        Power : 1
        CoefficientP : 1
        CoefficientQ : 0
        CoefficientD : 1
        Alternating : "true"
        PowerCoef : -10
        PowerShift : 9
        PolynomialP : [1]
        PolynomialQ : [-3 4]
    }
}

This provides access to y-cruncher's BinaryBBP Binary Splitting framework. This is an optimized special case of SeriesHypergeometric where Q(x) is a power-of-two multiple of R(x). All BBP-type formula with a base 2 radix will fall into this series type.

 

 

Computes:

Given:

The polynomials are arrays of the coefficients in increasing order of degree. The 1st element is the constant.

 

Computes one of the following depending on whether "Alternating" is true:

As with SeriesHypergeometric, this formula is slightly unconventional.

 

 

Basic Restrictions:

 

Polynomial Restrictions:

  1. P(x) and Q(x) are non-zero polynomials.
  2. Q(x) must be degree 1 or higher.
  3. Q(x) is of degree no higher than 62.
  4. The coefficients of both polynomials are signed 64-bit integers: [-263, 263)
  5. The coefficient of the highest degree is non-zero for both polynomials. (no leading zeros)
  6. Q(x) is non-zero for all positive integers.

Unlike the generic SeriesHypergeometric, the BinaryBBP series has no issues with irregular convergence or destructive cancellation.

 

 

Tips:

 

Performance Metrics:

Metric Complexity
Computational Cost O(n log(n)3)
Auxiliary Memory O(n)

 

Function Templates:

 

These are not built-in functions, but are templates for various functions.

 

 

ArcTan(1/x) - Taylor Series

These are useful for building Machin-like ArcTan() formulas for Pi.

Template using SeriesHypergeometric:

 

coefP = 1

coefQ = 1

coefD = x

P(k) = 1

Q(k) = -(2k+1) x2

R(k) = 2k+1

{
    SeriesHypergeometric : {
        CoefficientP : 1
        CoefficientQ : 1
        CoefficientD : x
        PolynomialP : [1]
        PolynomialQ : [-x2 -2x2]
        PolynomialR : [1 2]
    }
}

Unlike ArcCoth(x), y-cruncher has no native implementation of ArcTan(). It's not needed since nothing to date can touch Chudnovsky and Ramanujan's formulas.

 

ArcTan(1/x) - Euler Series

Euler's series for ArcTan() is slightly faster than the Taylor series.

Template using SeriesHypergeometric:

 

coefP = x

coefQ = x

coefD = 1+x2

P(k) = 2k

Q(k) = (2k+1)(1+x2)

R(k) = 2k

If x is an odd number, a factor of 2 can be removed from P(k), Q(k), and R(k).

{
    SeriesHypergeometric : {
        CoefficientP : x
        CoefficientQ : x
        CoefficientD : 1+x2
        PolynomialP : [0 2]
        PolynomialQ : [-1-x2 -2-2x2]
        PolynomialR : [0 2]
    }
}

See Pi - Machin.cfg for an example.

 

 

 

Deprecated:

 

Log-AGM: Natural Logarithm using AGM (Deprecated in: y-cruncher v0.8.4)

{
    Log-AGM : {
        Pi : "pi"
        Log2 : "log2"
        Argument: {...}
    }
}

Computes:

Natural logarithm of x using the AGM algorithm. This version of the Log function requires you to provide the constants Pi and Log(2) as variables.

 

Both constants Pi and Log(2) must already be defined in an enclosing scope using the specified names. Likewise, both constants must actually be the correct values of Pi and Log2 out to the full precision. Otherwise, the output will be incorrect.

 

The purpose of this function is to let you reuse the constants Pi and Log(2) so that they don't need to be recomputed if they are also needed elsewhere.

 

The following sample formulas use this function:

where:

Tips:

Performance Metrics:

Metric Complexity
Computational Cost 9.666 lg(n) M(n)
O(n log(n)2)
Auxiliary Memory O(n)

 

ArcSinlemn: Inverse Sine Lemniscate (Removed in: y-cruncher v0.8.3)

{
    ArcSinlemn : {
        Coefficient : 4
        x : 7
        y : 23
    }
}

Computes:

Coefficient * ArcSinlemn(x / y)

where:

Tips:

Performance Metrics:

Metric Complexity
Computational Cost O(n log(n)3)
Auxiliary Memory O(n)